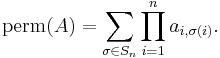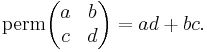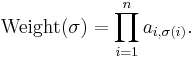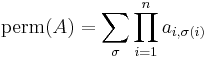Permanent

The permanent of a square matrix in linear algebra, is a function of the matrix similar to the determinant. The permanent, as well as the determinant, is a polynomial in the entries of the matrix. Both permanent and determinant are special cases of a more general function of a matrix called the immanant.

1 Definition
2 Properties and applications
3 Minimal permanent
4 Computation
5 See also
6 References
7 Further reading
8 External links

Definition

The permanent of an n-by-n matrix A = (a_i,j) is defined as

$\operatorname{perm}(A)=\sum_{\sigma\in S_n}\prod_{i=1}^n a_{i,\sigma(i)}.$

The sum here extends over all elements σ of the symmetric group S_n, i.e. over all permutations of the numbers 1, 2, ..., n.

For example (2×2 matrix),

$\operatorname{perm}\begin{pmatrix}a&b \\ c&d\end{pmatrix}=ad%2Bbc.$

The definition of the permanent of A differs from that of the determinant of A in that the signatures of the permutations are not taken into account. If one views the permanent as a map that takes n vectors as arguments, then it is a multilinear map and it is symmetric (meaning that any order of the vectors results in the same permanent). A formula similar to Laplace's for the development of a determinant along a row or column is also valid for the permanent; all signs have to be ignored for the permanent.

The permanent of a matrix A is denoted per A, perm A, or Per A, sometimes with parentheses around the argument. In his monograph, Minc (1984) uses Per(A) for the permanent of rectangular matrices, and uses per(A) when A is a square matrix. Muir (1882) uses the notation 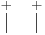$\overset{%2B}{|}\quad \overset{%2B}{|}$ .

The word, permanent originated with Cauchy (1812) as “fonctions symétriques permanentes” for a related type of functions, and was used by Muir (1882) in the modern, more specific, sense.

Properties and applications

Unlike the determinant, the permanent has no easy geometrical interpretation; it is mainly used in combinatorics and in treating boson Green's functions in quantum field theory. However, it has two graph-theoretic interpretations: as the sum of weights of cycle covers of a directed graph, and as the sum of weights of perfect matchings in a bipartite graph.

Cycle covers

Any square matrix 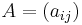$A = (a_{ij})$ can be viewed as the adjacency matrix of a directed graph, with 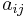$a_{ij}$ representing the weight of the edge from vertex i to vertex j. A cycle cover of a weighted directed graph is a collection of vertex-disjoint directed cycles in the graph that covers all nodes in the graph. 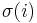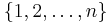Thus, each vertex i in the graph has a unique "successor" $\sigma(i)$ in the cycle cover, and $\sigma$ is a permutation on $\{1,2,\dots,n\}$ where n is the number of vertices in the graph. 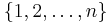Conversely, any permutation $\sigma$ on $\{1,2,\dots,n\}$ corresponds to a cycle cover in which there is an edge from vertex i to vertex 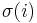$\sigma(i)$ for each i.

If the weight of a cycle-cover is defined to be the product of the weights of the edges in each cycle, then

$\operatorname{Weight}(\sigma) = \prod_{i=1}^n a_{i,\sigma(i)}.$

The permanent of an 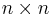$n \times n$ matrix A is defined as

$\operatorname{perm}(A)=\sum_\sigma \prod_{i=1}^{n} a_{i,\sigma(i)}$

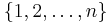where $\sigma$ is a permutation over $\{1,2,\dots,n\}$ . Thus the permanent of A is equal to the sum of the weights of all cycle-covers of the graph.

Perfect matchings

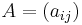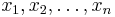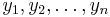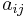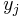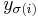A square matrix $A = (a_{ij})$ can also be viewed as the biadjacency matrix of a bipartite graph which has vertices $x_1, x_2, \dots, x_n$ on one side and $y_1, y_2, \dots, y_n$ on the other side, with $a_{ij}$ representing the weight of the edge from vertex $x_i$ to vertex $y_j$ . If the weight of a perfect matching $\sigma$ that matches $x_i$ to $y_{\sigma(i)}$ is defined to be the product of the weights of the edges in the matching, then

$\operatorname{Weight}(\sigma) = \prod_{i=1}^n a_{i,\sigma(i)}.$

Thus the permanent of A is equal to the sum of the weights of all perfect matchings of the graph.

0-1 permanents: counting in unweighted graphs

In an unweighted, directed, simple graph, if we set each 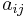$a_{ij}$ to be 1 if there is an edge from vertex i to vertex j, then each nonzero cycle cover has weight 1, and the adjacency matrix has 0-1 entries. Thus the permanent of a 01-matrix is equal to the number of cycle-covers of an unweighted directed graph.

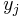For an unweighted bipartite graph, if we set a_i,j = 1 if there is an edge between the vertices $x_i$ and $y_j$ and a_i,j = 0 otherwise, then each perfect matching has weight 1. Thus the number of perfect matchings in G is equal to the permanent of matrix A.^[1]

Minimal permanent

Of all the doubly stochastic matrices, the matrix a_ij = 1/n (that is, the uniform matrix) has strictly the smallest permanent. This was conjectured by van der Waeden, and proved in the late 1970-s independently by Falikman and Egorychev.^[2] The proof of Egorychev is an application of the Alexandrov–Fenchel inequality.

Computation

Main articles: Computation of the permanent of a matrix and Permanent is sharp-P-complete

The permanent is believed to be more difficult to compute than the determinant. While the determinant can be computed in polynomial time by Gaussian elimination, Gaussian elimination cannot be used to compute the permanent. Moreover, computing the permanent of a 0-1 matrix (matrix whose entries are 0 or 1) is #P-complete. Thus, if the permanent can be computed in polynomial time by any method, then FP = #P, which is an even stronger statement than P = NP. When the entries of A are nonnegative, however, the permanent can be computed approximately in probabilistic polynomial time, up to an error of εM, where M is the value of the permanent and ε > 0 is arbitrary.^[3]

References

^ Dexter Kozen. The Design and Analysis of Algorithms. Springer-Verlag, New York, 1991. ISBN 9780387976877; pp. 141–142
^ Van der Waerden's permanent conjecture on PlanetMath
^ Jerrum, M.; Sinclair, A.; Vigoda, E. (2004), "A polynomial-time approximation algorithm for the permanent of a matrix with nonnegative entries", Journal of the ACM 51: 671–697, doi:10.1145/1008731.1008738

External links

Permanent at PlanetMath